반응형
1. 합병정렬(n개 수 랜덤 정렬)13,11,7,4,5,9,15,10
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#include <stdio.h>
void mergeSort(int data[], int p, int r);
void merge(int data[], int p, int q, int r);
int main() {
int data[8] = {13,11,7,4,5,9,15,10} , i;
printf("정렬 전\n");
for(i = 0; i < 8; i++) {
printf("%d ", data[i]);
}
printf("\n\n<<변화과정>>\n");
mergeSort(data, 0, data[i] - 1);
printf("\n정렬 후\n");
for(i = 0; i < 8; i++) {
printf("%d ", data[i]);
}
return 0;
}
void merge(int data[], int p, int q, int r) {
int i = p, j = q+1, k = p;
int tmp[8]; // 새 배열
while(i<=q && j<=r) {
if(data[i] <= data[j]) tmp[k++] = data[i++];
else tmp[k++] = data[j++];
}
while(i<=q) tmp[k++] = data[i++];
while(j<=r) tmp[k++] = data[j++];
for(int a = p; a<=r; a++) data[a] = tmp[a];
printf("\n 합병 >>");
for(int x=p;x<=r;x++){
printf("%d ",tmp[x]);
}
}
void mergeSort(int data[], int p, int r) {
int q;
printf("\n 분할 >>");
for(int x=p;x<=r;x++){
printf("%d ",data[x]);
}
if(p<r) {
q = (p+r)/2;
mergeSort(data, p , q);
mergeSort(data, q+1, r);
merge(data, p, q, r);
}
}
|
cs |
<결과>

=> 안정적인 정렬 가능하지만 / 레코드를 배열로 하면 임시공간이 필요하여 공간낭비가 생길 수 있다
===>>> 제자리 (in-place-sort) 해야함
2. 제자리 정렬 종류인 "선택 정렬" 사용 <java>
- 매 루프마다 최소값 또는 최대값을 선택해서 정렬하는 알고리즘
- 비교 기반 정렬 알고리즘
- 안정적이지 않은 정렬(동일한 키 값이 있을 경우 순서가 바뀔 수 있음)
- 최악, 최적, 평균 모두 O(n^2)의 수행시간을 보임
- 제자리 정렬
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class SelectionSort {
constructor(_list) {
const list = _list;
const swap = (list, a, b) => {
const temp = list[a];
list[a] = list[b];
list[b] = temp;
};
const selectionSort = list => {
if (Array.isArray(list)) {
if (list.length === 0) {
return [];
}
for (let i = 0; i < list.length; i++) {
let minIndex;
for (let j = i; j < list.length; j++) {
if (!minIndex || list[minIndex] > list[j]) {
minIndex = j;
}
console.log(j)
}
swap(list, i, minIndex);
}
return list;
}
};
return selectionSort(list);
}
}
//------------------------------------
const data = [14, 15, 17, 23, 8, 13, 11, 22];
const sortedData = new SelectionSort(data);
console.log(sortedData); // [8, 11, 13, 14, 15 17, 22, 23]
|
cs |
3. 도사 정리
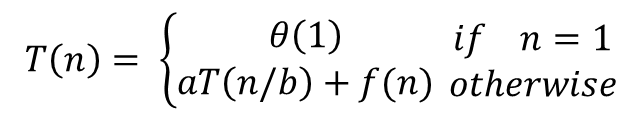
이 케이스를 나누는 방식은 a, b의 값을 바탕으로 계산한다.
<1번 경우>
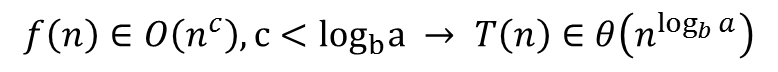
위와 같이 계산할 수 있다.
예를 들어 T(n) = 4*T(n/2) + n 이라면, a = 4, b = 2 이고 log_b a = 2이다. 이때 f(n)의 최고 차항이 1이므로 이 함수의 시간 복잡도는 theta(n^2)가 된다.
<2번 경우>
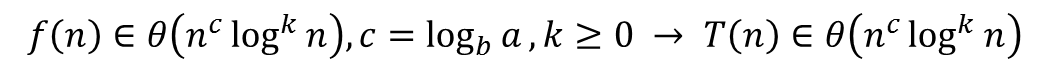
예를 들어 T(n) = 2*T(n/2) + n 이라면, a = 2, b= 2이고 c = 1이다. 따라서 시간 복잡도는 theta(n log n)이다.
<3번 경우>
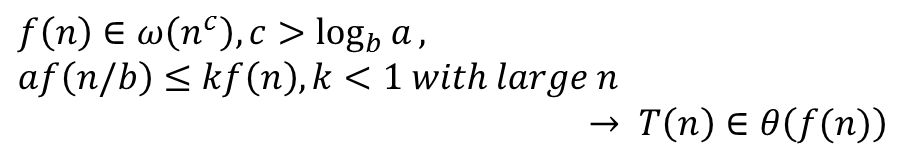

예를 들어 T(n) = 2*T(n/3) + n 이라면, log_b a 는 log_3 2 이면서, c는 1이다. 따라서 c > log_b a를 만족한다. 또한 2*(n/3) <= k(n)의 경우 2/3 <= k < 1을 만족하므로 시간 복잡도는 theta(n)가 된다.
<풀 수 없는 경우>
사실 저 형태의 시간복잡도가 아닌 함수는 빠르게 해결 할 수 없다. 예를 들어 T(n) = T(n/2) + T(n/4) + n 인 경우
트리 형태로 그려가면서 풀면 공비가 3/4인 등비수열의 합으로 나타낼 수 있다.
또한 멱급수나, 미적분을 해야하는 경우 또한 존재한다
반응형
'Algorithm Study > Algorithm' 카테고리의 다른 글
| 계수 정렬(Counting Sort)알고리즘 (0) | 2020.01.09 |
|---|---|
| 삽입 정렬(insertion sort) 알고리즘 (0) | 2020.01.04 |
| 선택 정렬(Selection sort) 알고리즘 (0) | 2020.01.04 |
| 버블 정렬(bubble sort) 알고리즘 (0) | 2020.01.04 |
| 피보나치 수열 합/시간 계산 알고리즘 (0) | 2019.03.10 |