exp_blog

1. 선택정렬

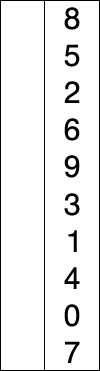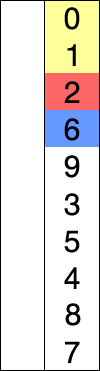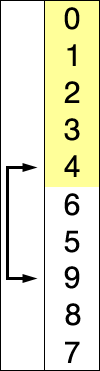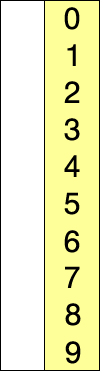
• 주어진 데이터 중 최소 값을 찾음
• 해당 최소값을 데이터 맨 앞에 위치한 값과 교체
• 맨 앞의 위치를 뺀 나머지 데이터를 동일한 방법으로 반복

2. 패턴 찾기

• data_list = [9,3,2,1]
  • 1회 : 1, 3, 2, 9
  • 2회 : 1, 2, 3, 9
  • 3회 : 1, 2, 3, 9

1. for stand in range(len(data_list) - 1) 로 반복
2. lowest = stand 로 놓고, //기준점이 맨 앞 최소값이니까 
3. for num in range(stand, len(data_list)) stand 이후부터 반복
   • 내부 반복문 안에서 data_list[lowest] > data_list[num] 이면,
     • lowest = num // 교환 해줌 
4. data_list[num], data_list[lowest] = data_list[lowest], data_list[num]

3. 알고리즘

def Selection_sort(data):
    for stand in range(len(data) - 1):
        lowest = stand
        for index in range(stand+1, len(data)):
            if(data[lowest]> data[index]):
                lowest = index
            data[lowest], data[stand] = data[stand], data[lowest]
    return data

import random

data_list = random.sample(range(50), 10)
Selection_sort(data_list)

>>[4, 12, 20, 27, 28, 25, 30, 39, 40, 43]

4. 알고리즘 분석

• 반복문이 두 개 O(𝑛2)
  • 실제로 상세하게 계산하면, 𝑛∗(𝑛−1)2

1. 정렬이란?

• 어떤 데이터들이 주어졌을 때, 정해진 순서대로 나열하는 것
• 다양한 정렬 알고리즘 이해를 통해 동일한 문제에 대한 다양한 알고리즘이 고안될 수 있고, 각 알고리즘 간 성능 비교를 통해 알고리즘 성능 분석도 이해할 수 있음

2. 버블 정렬(bubble sort)

• 두 인접한 데이터를 비교하여 앞에 있는 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘

## https://visualgo.net/en 사이트에서 보면 쉽게 그림으로 이해할 수 있다. 

3. 패턴 찾기

• 데이터가 4개 일 때 
  • data_list = [1,9.3.2]
    • 1차 로직
      • 1 vs 9 => X
      • 9 vs 3 => [1, 3, 9, 2]
      • 9 vs 2 => [1, 3, 2, 9]
    • 2차 로직
      • 1 vs 3 => X
      • 3 vs 2 => [1, 2, 3, 9]
      • 3 vs 9 => X
    • 3차 로직
      • 1 vs 2 => X
      • 2 vs 3 => X
      • 3 vs 9 => X

==> N 개의 리스트가 있는 경우 N-1 로직을 적용한다

==> 로직을 1번 적용할 때마다, 가장 큰 수가 뒤에서부터 1개씩 결정된다 

==> 로직이 일찍 끝날 수도 있다 

        => 로직을 적용 시,  한 번도 데이터가 교환되지 않는다면 이미 정렬된 상태므로 더 이상 로직을 반복 적용할

             필요가 없다 

==> 로직 한 회 끝날 때 마다 가장 큰 숫자가 뒤에서 1개씩 결정된다

4. 알고리즘

<프로토 타입>
1. for num in range(len(data_list)) 반복
2. swap = false // 교환되어있는지 확인,  false 가 기본값이여야 아래 for문에서 swap 이 멈춰야 알고리즘 종료
3. 반복문 안에서 , for index in range(len(data_list) - num - 1) 를 n-1번 반복해야한다 
    //num 을 빼는 이유는  data_list에서 로직이 돌면 맨 뒤에 가장 큰 값이 고정되기 때문에 
4. 반복문안의 반복문 안에서, if data_list[index] > data_list[index + 1]  이면
5. swap 시켜야한다
6. 더이상 swap 되지 않고 false 값이 나오면 break

def bubblesort(data):
    for index in range(len(data) - 1):
        swap = False
        for index2 in range(len(data) - index - 1):
            if data[index2] > data[index2 + 1]:
                data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
                swap = True
        
        if swap == False:
            break
    return data

import random

data_list = random.sample(range(50), 20)
bubblesort(data_list)

>>[3, 5, 10, 11, 18, 19, 20, 21, 24, 26, 28, 29, 31, 33, 34, 38, 39, 44, 46, 49]

5. 분석

• 반복문이 두개  :  O(𝑛2)
  • 최악 : 𝑛∗(𝑛−1)2
• 완전 정렬 되어 있으면 최선 : O(n)

셀렉트 문 쿼리 실행 시 성능을 좋게하려면 

1. 적절한 인덱스를 사용하여 Block I/O를 최소화하라.
2. 조인방법과 조인순서를 최적화 하라.
3. Table Access(Random Access)를 최소화하라.
4. Sort나 Gash 작업은 최소화하라.
5. 한 블록은 한번만 Scan하고 끝내라.
6. 온라인의 조회화면이라면 페이징처리는 필수이다.
7. 답이 틀리면 안된다. SQL을 검증하라

1. Hadoop 

• 정의 : 여러 대의 컴퓨터 클러스터(연결되어 하나의 시스템 처럼 동작하는 집합)에서 대규모 데이터 세트를 분산 처리 할 수 있게 해주는 프레임 워크 / 파일을 블록단위로 저장, 마스터 - 슬레이브 구조 
• 장점 : 멀티 노드로 부하를 분산시켜 처리 / 장비 추가 시 성능이 선형적으로 증가 / 저렴한 장비로 처리 가능 
• 분산 코디네이터 : Zookeeper
  • 중앙 집중식 서비스 / 알맞은 분산 처리 및 분산 환경을 구성하는 서버 설정을 통합적으로 관리 
• 분산 리소스 관리
  • YARN : 작업 스케줄링 및 클러스터 리소스 관리 위한 프레임워크 맵리듀스, 하이브, 임팔라, 스파크 등 다양한 APPLICATION이 안에서 작업 실행
  • Mesos : 클라우드 환경에 대한 리소스 관리
• 데이터 저장 
  • HBASE : 분산 데이터베이스 / 구글 빅테이블이 원조 
  • HDFS : 분산 파일 데이터 저장 / 자바로 작성된 확장 
  • Kudu : 컬럼 기반 스토리지 : 데이터에 대한 빠른 분석 위해 설계 
• 데이터 수집 
  • Chukwa : 분산 환경 생성되는 데이터 안정적으로 HDFS 에 저장하는 플랫폼 / 대규모 분산 시스템 모니터링 시스템
  • Flume : 많은 양 데이터 수집, 집계 및 이동위한 분산형 서비스 
  • Kafka : 데이터 스트림 실시간 관리, 대용량 이벤트 처리 위해 개발
• 데이터 처리
  • Mahout : 분석 기계학습에 필요한 알고리즘 구축
  • Spark  : 대규모 데이터 처리 위한 빠른 속도 실행시켜주는 엔진 / 파이썬, R 등에서 대화형으로 사용  / 메모리를 사용해 맵리듀스보다 빠르다 
  • HIVE : 하둡 기반 데이터 솔루션 / SQL과 유사한 HIVEQL 언어 제공하여 쉽게 데이터 분석 할 수 있게 도와줌
  • MapReduce : 대용량 데이터를 분산처리하기위한 프로그램 / 정렬된 데이터를 분산처리(키 , 밸류 쌍으로 구분)하여 Map 하고 이를 다시 합치는 Reduce (지표 생성)과정을 거친다 

2. Container (도커 / 쿠버네티스)

- 빅데이터에서 컨테이너(운영체제 커널을 공유하는 경량의 가상화 환경)와 하둡을 접목시키는 기술 증가 

3. Elastic Search 기반 데이터 수집  

• Logstash : 동적 데이터 수집 파이프라인
• ElasticSearch : 분산형 RESTFul 검색 및 분석 엔진
• kibana  : 엘라스틱서치 데이터 시각화

4. EC2 / RDS / Elastic Beanstalk / S3

• EC2 : 사용자가 아마존 머신 이미지로 부팅하여 인스턴스라고 불리는 가상 머신을 원 원하는 소프트웨어를 포함하여 구성하게 해줌 / 스케일링이 가능한 애플리케이션 배치 장려
• RDS : 분산 관계형 데이터베이스/ 관계형 DB의 스토리지, 연산 자원들을 스케일링 하는 것은 하나의 API 호출로 수행 / EC2와 함께 사용하여 DB 설정, 운영, 백업 기능 편하게 사용하는 DB 전용서버
• S3 : 저장 서비스 / 하나의 AWS 리전 내 물리적 가용영역에 자동으로 분산 저장 
• Elastic Beanstalk : EC2 + RDS 등 AWS 리소스 조합하여 완성된 어플리케이션 플랫폼  / PaaS

5. 의료 빅데이터 필요성 : DB 성능 확보하여 대용량 데이터를 기반으로 다양한 정보 분석 업무를 수행하여 의료 가치 있는 데이터 생성에 목적 / 시스템 성능 확보, 비정규화 및 테이블 병합 , 요약 테이블 적용, QL 튜닝 , 지속적인 성능 개선 활동 필요 

6. NoSQL 

- NOT ONLY SQL 

- RDBMS + 다른 특성 부가적으로 지원

- 기존의 관계형 데이터베이스보다 더 융통성 있는 데이터 모델 사용하고 데이터의 저장 및 검색 위한 특화된 매커니즘 제공 

- 특징

• 테이블 조인 기능 없음
• 비SQL 인터페이스 통한 데이터 액세스
• 여러 대의 DB 서버를 묶어 (클러스터링) 하나의 DB 구성
• ACID 미보장
• 스키마, 속성 동적 정의
• 중단 없는 서비스, 자동 복구 기능 지원
• 오픈소스
• 확장성 가용성 높은 성능 

- 종류 

• WIDE COLUMMAR STORE : 구글 Big Table Paper 에서 유래 / Key Value => Column Family 데이터 모델 사용 
  • HBASE / Cassandra/ ScyllaDB
• DOCUMENT DB : JSON, XML 같은 Collection 데이터 모델 구조 채택 
  • Mongodb

8. 머신러닝 R

- 머신러닝의 데이터 관리에 빅데이터를 사용할 수 있다.

- 대규모 데이터를 이용하기 위한 모델링을 컴퓨터가 알아서 하는 것이 머신러닝 

R  : 통계 처리 및 시각화 하는데 사용

9. 하둡 vs RDBMS 

• 데이터 타입 : 하둡(정형, 반정형, 비정형) / RDBMS (정형)
• 스키마 : 하둡(데이터 읽을 때 스키마 적용) / RDBMS(데이터 적재할 때 스키마 적용)
• 좋은 사용법 : 하둡(대용량 데이터 처리) / RDBMS(복잡한 ACID 트랜잭션에 적용)
• 속도 : 하둡(쓸 때 빠름) / RDBMS(읽을 때 빠름)

10. 빅데이터 4V?

속도 / 양 / 다양성 / 진실성(정확도 높아짐) / 가치

Telnet

- 원격 접속 서비스

- 특정 사용자가 네트워크 통해 다른 컴퓨터에 연결하여 그 컴퓨터에서 제공하는 서비스 받을 수 있는 인터넷 표준 프로토콜(컴퓨터, 네트워크 장비가 서로 통신하기 위한 규약)

ssh(Secure Shell)

- 세션을 감싸주는 텔넷 응용 프로그램

- 다른 사용자가 세션을 엿듣지 못하도록 => 암호화 되어 전송해 보안에 적합 

차이점

서버간의 통신 방법의 차이 (TCP / IP 패킷 정보 전달, 결과값 다시 서버에)

- TELNET : BYTE 스트림 형식으로 주고 받음 / 정보 노출 위험 큼 

- SSH : DES, RSA 등 고급 암호화 통해 통신 / 약간의 부하 생김 

##IP : 패킷 단위로 보낼 목적지 주소 할당 후 어디로 보낼지 결정하고 이를 전송 

    TCP :  IP 프로토콜 기반 위에서 전송되는 데이터들을 안정되게 전송 

1. 데이터 베이스 특징

• 독립성(물리적 / 논리적)
• 무결성(잘못된 데이터 발생 하는 경우 수 방지 => 유효성 검사 통해 구현)
• 보안성(인가된 사용자들만 자원에 접근)
• 일관성(연관된 정보 논리적 구조로 관리)
• 중복 최소화(자료 중복, 데이터 중복 문제 해결)

2. 데이터베이스 성능 

• 디스크 I/O 를 줄이는 것에서 시작
• 디스크 헤더 위치 이동 없이 얼마나 많은 데이터를 한번에 기록하느냐에 결정됨
• DB 쿼리 튜닝 : 랜덤 I/O 자체 줄여주는 것 목적

3. 인덱스 (= 색인)

• DBMS 에서 저장 성능 희생하여 데이터 읽기 속도 높이는 기능 
• 데이터가 정렬되어 들어간다 
• 양이 많은 테이블에서 일부 데이터만 불러 올 때, 풀 스캔 시 처리 성능 떨어짐 
• 종류
  • B +- Tree 인덱스 : 원래 값 이용해 인덱싱
  • Hash 인덱스 : 칼럼 값으로 해시 값 계산하여 인덱싱 / 메모리 기반 DB 에서 많이 사용 
  • B > Hash  -> 왜? ==> SELECT 질의 시 부등호 연산 포함되어 = 연산에 특화된 Hash는 적합하지 않다 
• 생성 시 고려 해야 할 점 
  • 테이블 전체 로우 수 15 % 이하 데이터 조회 시 생성
  • 테이블 건수가 적으면 인덱스 생성 X -> 풀 스캔이 빠름
  • 컬럼 : 유일성이 좋거나 범위가 넓은 값을 가지고 NULL 값이 많이 없는 것을 지정
  • 자주 쓰는 컬럼을 앞으로 지정 
  • DML(insert, delete, update) 시 인덱스에도 수정 작업이 동시에 발생하기에 많은 인덱스 생성 시 성능 부하 
  • DML 이 많은 테이블은 인덱스 생성 X
  • SQL 쿼리가 인덱스를 활용할 수 있게끔 짜기 

4. 클러스터 인덱스 vs 넌클러스터 인덱스 (oracle)

• 클러스터 인덱스 : 실제 DB의 데이터 파일에 정렬되어 있는 상태로 디스크 저장/  테이블 당 한개
                                   / 기본키 값이 비슷한 레코드 끼리 묶어 저장 
• 넌클러스터 인덱스 : 실제 DB의 데이터 파일에 정렬되지 않는 상태로 디스크 저장 / 테이블 당 여러 개 

5. 정규화 

• 중복 저장 시 갱신 이상 발생 -> 이를 해결하기 위해 정규화 과정 거침
• X의 값이 Y의 값을 유일하게 결정하면, "X는 Y를 함수적으로 결정"
• 갱신 이상 종류 
  • 삽입 이상 
  • 삭제 이상
  • 수정 이상
• 정규화란?
  • RDB 에서 중복을 최소화 하기 위해 데이터를 논리적으로 구조화하는 작업
  • 1NF : 원자값을 가진다
  • 2NF : 완전 함수적 종속 
  • 3NF : 이행적으로 종속되지 않는다
  • BCNF
• 단점 : JOIN 연산이 많아져 , 질의에 대한 응답시간이 느려질 수 있음 

6. 트랜잭션 

• 작업의 완전성 보장 
• 논리적 작업 셋이 모두 완벽하게 처리하거나 또는 처리하지 못할 경우 원상태로 복구해서 작업의 일부만 적용되는 현상 발생하지 않게 만들어주는 기능 
• 성질 : ACID(원자성 + 일관성 + 고립성 + 지속성)
• LOCK : 동시성 제어 VS 트랜잭션 : 데이터 정합성 보장 기능 

7. DeadLock

• 정의 : 두 개 이상의 트랜잭션이 특정 자원의 잠금(lock)을 획득한 채 다른 트랜잭션이 소유하고 있는 잠금을 요구하면 아무리 기다려도 상황이 바뀌지 않는 상태
• 빈도 낮추는 방법
  • 트랜잭션을 자주 커밋 
  • 정해진 순서로 테이블 접근
  • 읽기 잠금 획득 사용 피함
  • 복수 행의 연결에서 잠금을 획득해 갱신을 직렬화 하면 동시성은 떨어지지만 데드락 회피 가능 
• 데드락 발생 순서 
  • 트랜잭션 1 -> B t 첫번째 행 잠금 획득
  • 트랜잭션 2 => A t 첫번쨰 행 잠금 획득
  • 트랜잭션 commit 하지 않은 채 서로의 첫 번째 행에 대한 잠금 요청 시 데드락 발생

//잠금 획득 
Transaction 1> create table B (i1 int not null primary key) engine = innodb;
Transaction 2> create table A (i1 int not null primary key) engine = innodb;

Transaction 1> start transaction; insert into B values(1);
Transaction 2> start transaction; insert into A values(1);

//commit 없이 잠금 요청
Transaction 1> insert into A values(1);
Transaction 2> insert into B values(1);
ERROR 1213 (40001): Deadlock found when trying to get lock; try restarting transaction

8. VIEW

• 정의 : 물리적인 테이블을 근거한 논리적인 가상 테이블
• 이유 
  • 복잡하고 긴 쿼리문을 뷰로 정의하면 접근 단순화 시킬 수 있다
  • 보안 유리 

9. 데이터 무결성 제약조건 

• 정의 : 테이블에 부적절한 자료가 입력된 것을 방지하기 위해 컬럼에 대해 정의하는 여러 가지 규칙
• 무결성 제약 조건 종류
  • NOT NULL : NULL X
  • UNIQUE : 중복된 값 X / 항상 유일값
  • PK : NULL  X / 중복된 값 X  / 테이블 한 개에 유일하게 존재 
  • FK : 참조되는 테이블 칼럼 값 존재 시 허용 / 부모 키가 부모 테이블의 PK 나 UNIQUE 로 설정되어 있어야
  • CHECK : 저장 가능한 데이터 값의 범위 , 조건 지정해 설정한 값(타당한 값)만 허용 

10. 시퀀스(오라클)

• 시퀀스 생성 시 PK와 같이 유일한 숫자를 자동을 생성하는 발생기 
• 보통 PK로 설정하여 사용 
• 사용 이유 : 캐쉬에 상주하고 있어 데이터 불러오는 속도가 빠름 

11. 트리거

• 정의 : 자동으로 실행되게 정의한 저장 프로시저, INSERT / UPDATE/ DELETE 문에 대한 자동 호출
• 사용 이유 : 데이터 무결성 강화 / 업무 처리 자동화 / 업무 규칙 보장 

12. 데이터웨어하우스 

• DB 축적 데이터를 공통의 형식으로 변환해 의사결정에 도움 주는 DB

13. ORACLE DB VS MySQL

• ORACLE : 대규모 트랜잭션 처리 / 여러 서버에 대용량 DB 분산 / 절차 언어 통해 DB 내장 프로그램 작성 지원(트리거 , 독립실행)
• MySQL : 단일 DB / 대용량 DB X / DB 복원 저장점 없음 (COMMIT, ROLLBACK만 존재)

14. JOIN 

• 카티션 곱(Cartesian Product)
  • 두 개 이상의 테이블에 대해 연결 가능한 행을 모두 결합하는 조인 방법이며, WHERE 절에서 조인 조건절을 생략하거나 조인 조건을 잘못 설정하여 양쪽 테이블을 연결하여 조건에 만족하 는 행이 하나도 없는 경우에 발생 합니다. 
  • 예) SELECT * FROM DEPT A, EMP B 

•  EQUI JOIN
  • SQL 문에서 가장 많이 사용되는 조인으로 조인 대상 테이블에서 공통 칼럼을 ‘=’ 비교를 통해 같은 값을 갖는 행에 대해서 연결하여 결과를 생성하는 조인 방법입니다.
  • 예) SELECT A.name FROM DEPT A, EMP B WHERE A.code = B.code 

•  NON-EQUI JOIN
  •  조인 조건에서 ‘<’,’>’, BETWEEN a AND b’와 같이 ‘=’ 조건이 아닌 다른 종류의 연산자를 사용 하는 조인 방법입니다.
  • 예) SELECT A.name FROM DEPT A, EMP B WHERE A.code > B.code

•   OUTER JOIN
  • 두 개 이상의 테이블 조인 시 한쪽 테이블의 행에 대해 다른 쪽 테이블에 일치하는 행이 없더 라도 다른 쪽 테이블의 행을 NULL로 하여 행을 Return하는 것이 OUTER JOIN 입니다.연산자 로는 (+)기호를 사용합니다.
  • 조인 조건에 만족하지 않는 행도 나타냄 
  • 예) SELECT A.name FROM DEPT A, EMP B WHERE A.code = B.code(+)

•   SELF JOIN
  • 한 테이블 내 두 개의 칼럼을 연결하여 EQUI JOIN을 하는 방법

15. DB 설계 시 중요

• 무결성을 보장하는 것
• 무결성 보장 방법
  • (애플리케이션) 데이터를 조작하는 프로그램 내에서 데이터 생성, 수정, 삭제 시 무결성 조건 검증
  • (DB트리거) 트리거 이벤트 시 저장 SQL실행, 무결성 조건 실행
  • (제약조건) DB제약조건 기능 선언하여 무결성 유지

16. SQL 문장 종류

17. 데이터 유형

1. Spring이란?

자바 플랫폼을 위한 오픈 소스 애플리케이션 프레임워크

종속 객체를 생성해주고 조립해주는 도구 

• 특징
  • 경량 컨테이너로 각각의 객체 생성, 소멸과 같은 라이프 사이클을 관리하여 스프링으로 부터 필요한 객체 얻어 옴
  • POJO (Plain Old Java Object) 방식 프레임워크
    • 특정 인터페이스를 구현하거나 상속받을 필요 없어, 기존에 존재하는 라이브러리 등을 지원해, 용이하고 가벼움
  • 제어 역행(IOC) 기술 사용해 애플리케이션의 느슨한 결합 도모 
    • 컨드롤의 제어권이 프레임워크에 있어, 필요에 따라 스프링에 사용자의 코드 호출
  • 관점 지향 프로그래밍(AOP) 위한 풍부한 지원
    • 트랜잭션, 로깅, 보안 과 같이 여러 모듈에서 공통적으로 사용하는 기능의 경우 , 따로 분리하여 관리할 수 있음
  • 의존성 주입(DI) 지원
    • 각각의 계층이나 서비스들 간에 의존성이 존재할 경우 프레임워크 서로 연결
  • 확장성이 높음

2. 스프링에서 공통 부분 관리

• Filter  : 요청, 응답 거른 뒤 정제 / 스프링 컨텍스트 외부에 존재, 스프링과 무관한 자원에 동작
• Interceptor  : 스프링의 DistpatcherServlet 이 컨트롤러를 호출하기 전, 후 끼어듬
                             스프링컨텍스트내부에서 Controller 요청, 응답 처리 
                             여러 개 사용 가능 
• AOP : 로깅, 트랜잭션, 에러 처리 등 메서드 에서 조금 더 세밀하게 조정 

3. MVC 패턴(MODEL, VIEW, CONTROLLER)

model1 : 구분 필요없는 내용 / 주먹구구식, 작은 프로그램

model2 : 내용, 형식에 따라서 파일을 분류해서 프로그래밍 (MVC) /여러명이 작업

MODEL

• 논리적 데이터 기반 구조 표현
• 데이터와 관련된 저장, 가공
• 데이터베이스, 처음 정의하는 상수, 초기값, 변수 
• 사용자가 편집하길 원하는 모든 데이터를 가지고 있어야 함
• 뷰, 컨트롤러에 대해 어떤 정보도 알지 말아야 한다
• 변경 일어나면, 변경 통지에 대한 처리 방법을 구현

VIEW

• 사용자에게 보여지는 화면 
• 컨트롤러에 값을 받고 화면에 보여줌 
• 모델이 가지고 있는 정보를 따로 저장해서는 안된다.
• 모델이나 컨트롤러 같이 다른 구성 요소들을 몰라야한다
• 변경이 일어나면 변경통지에 대한 처리 방법 구현

Controller

• model, view 내의 클래스들 간 정보 교환
• model, view를 가지고 있어 값을 처리하고 화면에 보여주는 것 
• 데이터와 사용자인터페이스 요소들을 잇는 다리 역할
• 모델, 뷰에 대해 알고 있어야 한다.
• 모델, 뷰 변경 모니터링

서로 분리하여 각자의 역할에 집중하게 개발하고 유지 보수성, 애플리케이션 확장성, 유연성이 증가하고 , 중복코딩 또한 사라진다

4. 장고 VS 스프링

장고 

• PYTHON + MVC 패턴 + 관습 지향 + ORM + 라이브러리 => 완전 고수준 프레임워크
• 스크립트 언어 사용하기에 디버깅이 굉장히 수훨 
• 동시요청 처리능력은 좋지 않음
• 주요 기능
  • MVC 패턴 기반 MVT
  • ORM(Object relational mapping)

스프링

• JAVA Servlet + MVC 패턴 + DI, AOP + 라이브러리
• 아파치 + 톰캣 + 스프링 + MYSQL 조합
• 컴파일 언어 이기에 배포가 까다로움
• 주요 기능
• DI (Dependency Injection) : 의존 관계 주입
  •  각각의 계층이나 서비스 간에 의존성이 존재할 경우 Spring이 서로 연결시켜 준다.

• AOP (Aspect Orientated Programming) : 관점 중심 프로그래밍
  •  여러 곳에서 공통적으로 쓰이는 기능들을 분리하여 개발하고 실행 시에 서로 조합할 수 있는 AOP를 지원한다.

<알고리즘>

1. array,  linked list

배열 : 데이터를 물리적 주소에 순차적으로 저장, 인덱스를 가지고 있으며 특정 데이터에 바로 접근할 수 있어 속도가 빠르다

연결리스트 : 데이터를 저장할 때 데이터 + 다음 데이터 물리적 주소까지 같이 저장  / 첫 노드 부터 원하는 노드까지 링크를 따라가야 접근 가능하기에 접근 속도는 떨어짐 

• 속도 : 데이터에 대한 접근 속도 (배열 > 연결리스트)
  • 배열 : index 만 있으면 O(1) 접근
  • 연결리스트 : 최소 한 번은 리스트를 순회하여야 하므로, O(n)에 접근
• 데이터 삽입 속도 : 경우에 따라 다르지만(전체적으로 배열 < 연결리스트)
  • 배열에 공간이 많이 남아있고 맨 끝에 삽입 한다면 O(1)이 가능하지만 매우 드뭄
    • 배열은 중간, 맨 앞에 삽입 할 경우 데이터를 한 칸씩 미뤄야 하고
    • 데이터 삽입 시 모든 공간이 다 차버렸다면, realloc() 또는 새로이 할당하여 메모리 공간 확장 필요
  • 연결리스트 : 어느 곳에 삽입하던지 O(n) 시간 접근 
• 데이터 삭제 속도 : 경우에 따라 다르지만(전체적으로 배열 < 연결리스트)
  • 위와 비슷하다
  • 연결리스트의 경우 예외 조건 처리를 꼼꼼히 필요로 함 
• 삽입 삭제가 빈번하다면 연결리스트의 , 이미 만들어진 구조에서 데이터 접근만 필요로 하면 배열

2. 버블 정렬

서로 인접한 두 원소를 검사하여 정렬하는 알고리즘(인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환)

• 특징 
  • 장점 : 구현이 매우 간단
  • 단점 : 순서에 맞지 않은 요소를 인접한 요소와 교환 / 배열에서 모든 요소들과 교환해야 왼쪽 -> 오른쪽으로 이동 가능

3. 퀵 정렬

• 리스트 안에 있는 한 요소(피벗) 를 가지고 이를 기준으로 삼아 분할하고 분할된 부분 리스트 정렬 후 
  두 개의 정렬된 부분 리스트를 합하여 전체 리스트 한다
• 분할-> 정복 -> 결합 

4. 힙 정렬

• 완전 이진 트리 이용해 내림차순 기준으로 정렬

5. 합병 정렬

• 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬 , 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법 
• 분할 -> 정복 -> 결합

6. ArrayList<>란

 : 배열의 확장판. 배열의 크기를 임의적으로 변화시킬 수 있음, list에 들어갈 데이터 타입 설정 가능

    (add, remove, isEmpty, size, get, indexOf 등의 메소드가 있음)

7. hash란?

 : 내부적으로 배열을 사용(HashTable)하여 데이터를 저장, 검색 속도가 빠름.

 데이터 삽입/삭제시 기존 데이터를 밀어내거나 채우지 않고, 데이터와 연관된 고유한 숫자를 생성해 이를 인덱스로 사용.

8. equals와 HashCode?

(equals) 동일한 내용을 가진 객체인지를 비교

(hashcode) 동일한 객체인지 구별하기 위해 고유한 정수 값으로 출력

9. 스택과 큐의 차이

: (stack) Last in First out

   -> 함수를 호출 할 때, 현재 함수에서 사용되는 값을 스택에 넣고, 작업이 끝나면 함수를 리턴하고 스택에 넣었던

       값을 꺼내는 방식으로 동작

 (Queue) First in First out 

   ->프로세스 처리, CPU 관리, 프린터 큐 등에 사용